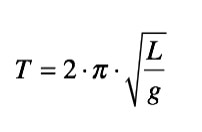|
Screencasts avec résolutions de problèmes de physique : les ondes |
Ondes planes à la surface de l'eau (En phase / opposition de phase)
|
Un vibreur de fréquence 50 Hz provoque des ondes circulaires à la surface de l'eau d'une cuve à ondes. La célérité des ondes vaut 0,4 m/s. On se propose d'observer le phénomène sous éclairage stroboscopique.
1) Sur quelle fréquence minimale convient-il de régler le stroboscope pour qu'une crête prenne la place d'une autre crête entre chaque éclair. 2) Sur quelle fréquence faut-il régler le stroboscope pour qu'entre deux éclairs une crête prenne la place d'un creux, et ce, de proche en proche. 3) Le stroboscope est réglé sur une fréquence de 49 Hz, la fréquence du mouvement est de 50 Hz. De combien progresse chaque circonférence de crête entre deux éclairs ? 4) Le stroboscope est réglé sur une fréquence de 49 Hz. De quelle distance apparente l'observateur estime-t-il voir progresser chaque circonférence entre deux éclairs ? 5) Le stroboscope est réglé sur une fréquence de 49 Hz. Calculer la célérité apparente de l'onde progressive. 6) Exprimer cette célérité apparente en fonction de la célérité réelle et des fréquences 𝝂 et 𝝂e du vibreur et des éclairs. 7) Sur quelle fréquence faut-il régler le stroboscope pour que la célérité apparente soit 100 fois plus faible que la célérité réelle. |
|
Fréquences (En phase / opposition de phase)
|
Un haut-parleur assimilé à une source ponctuelle S est alimenté par un générateur basse fréquence. La fréquence des vibrations électriques appliquées à l'entrée du haut-parleur sont réglable.
Les ondes sonores émises sont assimilées à des ondes sphériques dont la célérité est constante dans toutes les directions. ( c= 340 m/s) a) En un point M situé à la distance d=2m de S, on place un micro, lui aussi considéré comme ponctuel. Pour quelles fréquences les vibrations du haut-parleur et du micro sont-elles en phase? Pour quelles fréquences les vibrations du haut-parleur et du micro sont-elles en opposition de phase? b) On fixe la fréquence à 510 Hz. Préciser la position des points vibrant en phase avec le point M. Quel en est le nombre sur le segment SM . On modifie la fréquence qui devient 550 Hz. De quelles distances minimales faut-il rapprocher ou éloigner le micro sur la droite SM pour détecter une vibration sonore en phase avec la source. |
|
Célérité du son dans un gaz
Rechercher la fréquence sur un oscilloscope
|
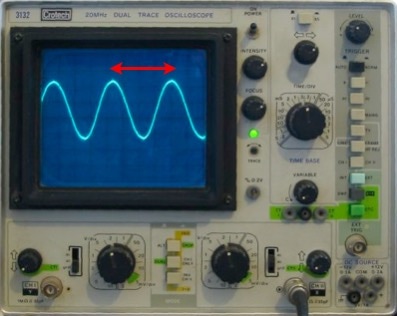
Un professeur capte des signaux venant de l’Espace sur l'écran d'un oscilloscope dont la fréquence de balayage est de 300 Hz. On observe 3 oscillations sur l'écran.
a) Quelle est la fréquence des vibrations de l'émetteur? b) Quelle fréquence de balayage faut-il adopter pour n'observer qu'une oscillation à l'écran? |
|
Botafumeiro de Saint-Jacques de Compostelle: pendule
|
Pendant qu'on le balance comme s'il s'agissait d'un pendule, huit hommes «tiraboleiros» donnent de la corde au point le plus élevé du mouvement et tirent sur elle au point le plus bas. On accroît ainsi l'oscillation de l'encensoir pour l'élever à 20,6 mètres de haut dans la voûte, en formant un arc de 65 mètres tout au long du transept. Il passe au ras du sol à une vitesse de 68 km/h en laissant derrière lui un fin sillage de fumée et d'encens.
Cet encensoir avait pour objectif de parfumer la cathédrale en raison du nombre important de pèlerins arrivant chaque année, durant le Moyen Âge puis à la Renaissance. L'odeur générée par la masse des dormeurs dans la nef nécessitait un encensoir de cette taille et de ce poids. Calculer la longueur de la corde si la période de l'oscillation de l'encensoir est de 9,5 s On montre que la période des oscillations est donnée par la relation: L: longueur du fil g: intensité du champ de la pesanteur (9,81 m/s2) |
|
Elongation - Equation horaire (un rasoir)
|
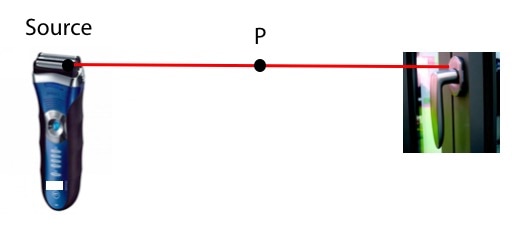
Un rasoir raccordé à une fine corde produit des vibrations entretenues de 2 mm d’amplitude à la fréquence 50 Hz. Les vibrations se propagent à la célérité de 250 mm/s. (voir expérience au cours de physique). On suppose qu’il n’y a pas de réflexion des ondes sur l’obstacle.
a) Rechercher la longueur d’onde b) Ecrire l’équation horaire d’un point P (= élongation pour un point P) c) Rechercher l’élongation d’un point P situé à 4,8 cm de la source à l’instant t=1,5 s d) Rechercher l’équation de la vitesse au point P. |
|
Célérités différentes (signaux dans un tuyau)
|
Un élève frappe sur une extrémité d’un tuyau de longueur «L» avec un marteau provoquant un «bang» (signal) capable de se propager dans l'air et dans le tuyau en fonte. Un autre élève capte le «bang» à l’autre bout du tuyau.
Quelle doit être la longueur du tuyau pour que l'oreille appliquée à l'autre extrémité du tuyau puisse distinguer les sons propagés dans l'air et dans la fonte? On donne: la célérité du son : dans l'air: c=340m/s et dans la fonte: c=5000m/s L'oreille a une certaine "inertie" (persistance des impressions sonores); elle ne peut distinguer deux sons que s'ils lui parviennent séparés par un laps de temps minimal de 0,1s. |
|
Niveau d’intensité sonore
|
Les vuvuzelas, ces longues trompettes en plastique indispensables à tout supporteur sud-africain, risquent d'endommager définitivement l'ouïe des amateurs de foot selon une étude.
Des tests menés par un fabricant de prothèses auditives ont abouti à la conclusion que les «vuvuzelas» émettaient un son de 127 décibels. Rechercher l’intensité du son quand 30 amateurs de foot jouent en même temps du vuvuzela. |
|
Corde de guitare, onde progressive
|
Une corde de guitare oscille entre deux positions extrêmes distantes de 3 mm. Quand l’expérimenter déclenche le chrono, la position du point P (au milieu de la corde) se trouve à - 0,8 mm de la position d’équilibre. la fréquence d’oscillation de la corde est de 8 Hz.
|
|