|
Screencasts avec résolutions de problèmes de physique : magnétisme |
Exercice 1
|
Un faisceau d’électrons homocinétiques (v0=10E7 m/s) pénètre orthogonalement au vecteur B dans une région où règne un champ magnétique uniforme (B=T).
La masse des électrons est de 9,1E-31 kg a)Calculer le rayon de la trajectoire circulaire b)Calculer le temps mis par les électrons pour faire la moitié d’un tour sur leur trajectoire |
|
Le spectrographe de masse
|
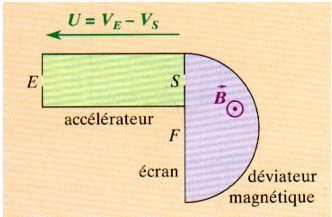
On se propose de séparer des noyaux d’hélium de masse m1=5E-27 kg et de masse m2 = 6,7 E-27 kg. Ces noyaux pénètrent en E dans un accélérateur avec une vitesse considérée comme nulle. Ils y sont accélérés par une tension U=VE -VS = 10 kV établie entre les plaques d’entrée et de sortie.
En S, ils quittent l’accélérateur avec une vitesse acquise, perpendiculaire à la plaque de sortie, et entrent dans le déviateur magnétique. Dans ce dernier, ils sont soumis à un champ magnétique uniforme perpendiculaire au plan de la figure. Ils sont enfin reçus sur un écran fluorescent F. a)Déterminer en fonction de q et U la vitesse v1 de l’ion de masse m1 et la vitesse v2 b)Rechercher l’expression littérale de leurs rayons R1 et R2 en fonction de m1 ou m2 et de q, U et B. Calculer R1 et R2 sachant que B=0,5T c)A1 désigne le point d’impact des noyaux sur l’écran et A2 celui des noyaux . Calculer la distance A1A2. |
|
Le cyclotron
|
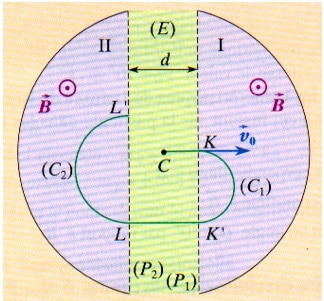
une particule, de masse m et de charge q, pénètre en C, avec une vitesse négligeable, dans un espace où règne un champ électrique . Cet espace est limité par deux grilles planes P1 et P2, assimilables à deux plaques métalliques distantes de d. On applique entre ces deux plaques une tension électrique UP1P2 positive. La particule se déplace de C vers K où elle arrive avec une vitesse .
De part et d’autre des grilles règne un champ magnétique uniforme et constant, perpendiculaire au plan de la figure. La particule pénètre au point K dans la région I avec la vitesse précédente. Elle décrit alors une trajectoire circulaire ( C1). |
|
1) Exprimer l’énergie cinétique de la particule en K’ en fonction de m et v0, suite à la différence de potentiel U. Quel est le rôle du champ magnétique
2)Exprimer le rayon R1 de la trajectoire (C1) en fonction de m,q, v0 et B
Lorsque la particule est dans l’espace I, le signe de la tension UP1P2 change de signe. Entre (P1) et (P2) la particule est animée d’un mouvement rectiligne uniformément accéléré et devient la trajectoire K’L. Exprimer son énergie cinétique en L en fonction de m, q, v0 et UP1P2. Quel est l’intérêt du passage de la particule dans la zone (E)
3)La particule décrit ensuite une trajectoire circulaire (C2). Exprimer le rayon R2 de la trajectoire (C2) en fonction de m, q, v0 , B et U.
4)Exprimer la durée du demi-tour LL’ et la comparer à la durée du demi-tour KK’.
2)Exprimer le rayon R1 de la trajectoire (C1) en fonction de m,q, v0 et B
Lorsque la particule est dans l’espace I, le signe de la tension UP1P2 change de signe. Entre (P1) et (P2) la particule est animée d’un mouvement rectiligne uniformément accéléré et devient la trajectoire K’L. Exprimer son énergie cinétique en L en fonction de m, q, v0 et UP1P2. Quel est l’intérêt du passage de la particule dans la zone (E)
3)La particule décrit ensuite une trajectoire circulaire (C2). Exprimer le rayon R2 de la trajectoire (C2) en fonction de m, q, v0 , B et U.
4)Exprimer la durée du demi-tour LL’ et la comparer à la durée du demi-tour KK’.